Kwintenstappen in toonladders (1)
Majeur, Mineur en de C-blues toonladder
Tekst en afbeeldingen: Marjan Waldorp
Artikel uit Turning Wheel 2024-4
Iets van het wonder van muziek begrijpen, dat was voor mij zo'n tien jaar geleden de belangrijkste drijfveer om me in muziek te gaan verdiepen. Ik schafte een keyboard aan om intervallen na te kunnen spelen en zo te analyseren wat ik gehoord had. Ja, ik ben ook gaan leren speler, eerst piano op het keyboard en vervolgens Hammond via de SetBfree emulatie, maar muziek is voor mij ook spelen en experimenteren met muziek, doorgronden.
Van meet af aan wilde ik eigenlijk jazz spelen, echter zonder enige basis gaat dat natuurlijk niet. Ik was dan ook heel blij met de pianoboekjes "Het Aanwijssysteem" van mijn schoonmoeder. Maar nu ik het eerste boekje uit heb, wil ik een nieuwe poging doen de "eenvoudige" Hammond jazz video's van Tony Monaco te volgen. Om te beginnen ben ik maar eens zijn video over de "C-blues scale" gaan bekijken, een belangrijk raamwerk voor jazzimprovisatie, of zoals Tony het zelf zegt: "The C-blues scale is not a scale. It is a language to express yourself".
De C-blues toonladder is een eigenaardige opeenvolging van tonen en intervallen. De (Engelse) Wikipedia schrijft dat de Bluestoonladder een mineur pentatonische toonladder is, aangevuld met een extra "blue" noot tussen de 4e en 5e trap in. Bij de C-blues toonladder is dat de F# (of Gb). De C-mineur pentatonische toonladder is te construeren uit vijf opeenvolgende kwinten van de kwintencircel: G, C, F, Bb, Eb. Daarbij is G, vanuit de grondtoon C gezien, één stap rechtsom en Eb drie stappen linksom. Een dergelijke opbouw uit kwintenstappen klinkt logisch. Immers, de kwint is met zijn frequentieverhouding van 3:2 het meest consonante interval na het octaaf (2:1). Consoneren betekent "goed samenklinken". Ons brein houdt van orde en regelmaat, structuur. Dan "begrijpen" we het. We hebben er grip op. Zo kijken we graag naar bollenvelden met hun regelmatige straten, prachtig! Eenvoudige frequentieverhoudingen vinden we goed klinken.
Pythagoras
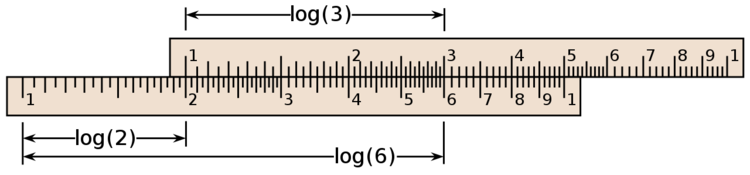
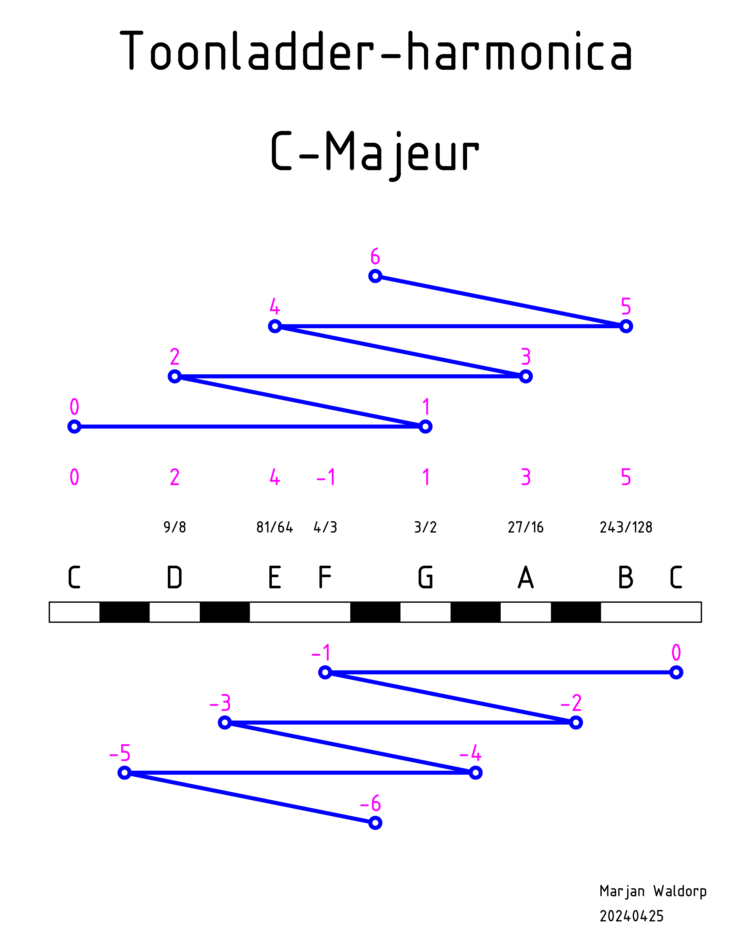
Kunnen heptatonische (gewone) toonladders eveneens uit opeenvolgende kwinten geconstrueerd worden? Ja, zeker! In de figuur "Toonladder-harmonica C-Majeur" heb ik de constructie uitgetekend. Een toonladder is een logaritmische schaal, zoals een rekenlineaal: optellen is vermenigvuldigen (zie figuur rekenlineaal). Als we in de eerste stap de grondtoon C met een kwint verhogen, vermenigvuldigen we de frequentie van de grondtoon met 3/2. Als we in de tweede stap de grondtoon nogmaals met een kwint verhogen, komen we op een frequentie van 3/2 x 3/2 = 9/4 maal de grondtoon. Wanneer we dit vervolgens een octaaf verlagen, delen we de frequentie door 2 en komen op 9/8. Na de derde kwintenstap komen we op 9/8 x 3/2 = 27/16. Na de vierde stap op 27/16 x 3/2 x 1/2 = 81/64. Na de vijfde stap op 81/64 x 3/2 = 243/128.
Duidelijk te zien is dat de uit deze zig-zag constructie voortkomende toonladder ongelijke toonsafstanden heeft! De toonlader heeft hele en halve toonsafstanden (diatonische toonladder). In de eerste kwintenstap C-G tekent zich dit patroon al onvermijdelijk af. Een kwint is 3 1/2 toonsafstand. Een octaaf is 6 hele toonsafstanden. Dus de toonladder zal minimaal twee halve toonsafstanden moeten bevatten. Voor de C-Majeur toonladder resulteert het verder zig-zaggen in het patroon 2 1/2 + 3 1/2. Dit verklaart ook de kenmerkende structuur van het klavier met een blokje van drie witte en twee zwarte toetsen, gevolgd door een blokje van vier witte en drie zwarte toetsen. Het komt allemaal door de kwint!
In feite is deze met kwintenstappen gebouwde toonladder dezelfde toonladder, zoals die geconstrueerd werd door Pythagoras (ca. 500 v. Chr.!). Zij het dat Pythagoras zijn constructie vanuit het midden van de toonladder begon, waardoor de grondtoon niet de naam "A" maar "C" heeft gekregen. De toonladder van Pythagoras is gebaseerd op de eerste drie priemgetallen:
| 1: | prime (de toon zelf) |
| 2: | octaaf (x2) |
| 3: | kwint (x3/2) |
Priemgetallen hebben de eigenschap dat zij alleen deelbaar zijn door 1 en door zichzelf. En hiermee heeft de toonladder van Pythagoras een conceptueel probleem. Geen enkele macht van het priemgetal 3 zal deelbaar zijn door 2. Dus het stapelen van kwinten kan nooit op een veelvoud van octaven uitkomen! In de kwintencircel komen we na 12 stappen weer op C. Maar die C is niet dezelfde C als die van het begin. Twaalf zig-zag kwintenstappen is in frequentie: (3/2)12 / (2)6 = 312 / 218 = 531441 / 262144 = 2,0262. Dat is dus net iets meer dan 1 octaaf (de zgn. Pythagoreïsche komma). De oplossing is de kwint iets te verkleinen, zodat (2k)12 = 524288. De verkleinde kwint wordt dan: 1,4983 (-0,11%). Dit is de kwint in de "gelijkzwevende stemming", zoals die vandaag alom wordt toegepast.
Kwintenstappen en consonantie
Hoe consonant zijn de tonen van de C-Majeur toonladder t.o.v. de grondtoon? Het meest consonant is natuurlijk de grondtoon C zelf en zijn evenknie één octaaf hoger. Daarna komen de G, één kwintenstap rechtsom in de kwintencircel, en de F, één kwintenstap linksom in de kwintencircel. De F en de G zijn elkaars spiegelbeeld. De F is een kwart (4/3) vanuit de grondtoon C en een kwint (3/2) vanuit de C, één octaaf hoger. Bij de G is dit precies andersom. Kwart (4/3) en kwint (3/2) zijn samen een octaaf: 4/3 x 3/2 = 2. De G en de F zijn door hun consonante verhouding met de grondtoon belangrijke tonen in de toonladder. De G heeft de naam "dominant" en de F "subdominant". De grondtoon C zelf heet de "tonica" van de toonladder.
Met meer kwintenstappen wordt het verband met de grondtoon C minder duidelijk. De tweede kwintenstap brengt ons op 9/8 (D), de derde op 27/16 (A), de vierde op 81/64 (E) en de vijfde op 243/128 (B). De D, een secunde vanuit de grondtoon, is met twee kwintenstappen veel minder consonant t.o.v. de grondtoon (9/8) dan de G en de F met één kwintenstap. Zijn de uit de derde en vierde kwintenstap voortkomende tonen A en E weer minder consonant t.o.v. de grondtoon dan de D met twee kwintenstappen? De frequentie van E, een grote terts vanuit de grondtoon, ziet er op het eerste gezicht niet erg consonant uit: 81/64. Wanneer we echter priemgetal "5" erbij betrekken, is 81/64 niet veel verwijderd van 80/64. Die breuk laat zich vereenvoudigen tot 5/4 en dat is een consonantere verhouding dan 9/8!
| E grote terts | Frequentie | Decimaal | Afwijking |
|---|---|---|---|
| Pythagoras +4 | 81/64 | 1,2656 | +1,25% |
| Reine stemming | 5/4 | 1,25 | - |
| Gelijkzwevend | 24/12 | 1,2599 | +0,79% |
De derde kwintenstap brengt ons op de A. Wanneer we de kortste afstand tot de grondtoon nemen, is de A een kleine terts lager dan de C één octaaf hoger. De frequentie van het interval A-C is: 2 / (27/16) = 32/27. Die frequentie blijkt zeer dicht bij de verhouding 6/5 te liggen en dat is wederom consonanter dan 9/8!
| A-C kleine terts | Frequentie | Decimaal | Afwijking |
|---|---|---|---|
| Pythagoras +3 | 32/27 | 1,1852 | -0,34% |
| Reine stemming | 6/5 | 1,2 | - |
| Gelijkzwevend | 23/12 | 1,1892 | -0,90% |
Na vijf kwintenstappen komen we op B, een halve toonsafstand lager dan de C één octaaf hoger. De frequentie van het interval B-C is: 2 / (243/128) = 256/243. Dat ligt dicht bij de verhouding 16/15 en dat is minder consonant dan 9/8.
| B-C kleine secunde | Frequentie | Decimaal | Afwijking |
|---|---|---|---|
| Pythagoras +5 | 256/243 | 1,0535 | -1,24% |
| Reine stemming | 16/15 | 1,0667 | - |
| Gelijkzwevend | 21/12 | 1,0595 | -0,68% |
Wanneer we het aantal kwintenstappen ordenen in afnemende consonantie, kunnen we nu de volgende staat opstellen:
| K | Interval | Rein | +/- Pythagoras | |
|---|---|---|---|---|
| 1 | Kwint | C-G | 3/2 | |
| 4 | Grote terts | C-E | 5/4 | (+1,25%) |
| 3 | Kleine terts | A-C | 6/5 | (-0,34%) |
| 2 | Secunde | C-D | 9/8 | |
| 5 | Kleine secunde | B-C | 16/15 | (-1,24%) |
Zarlino
Met de zoektocht naar goed samenklinkende frequentieverhoudingen hebben we stilzwijgend afstand genomen van de toonladder van Pythagoras en zijn we uitgekomen bij de toonladder van Zarlino. Gioseffo Zarlino (16e eeuw) deelde de snaar op in zes gelijke delen. Hieruit leidde hij de belangrijkste intervallen af:
| 2:1 | Octaaf |
| 3:2 | Kwint |
| 4:3 | Kwart |
| 5:4 | Grote terts |
| 6:5 | Kleine terts |
De terts kreeg dus zijn eigen verhouding (5:4) en daarmee brak Zarlino met de terts van Pythagoras als de som van twee secundes: 9/8 x 9/8 = 81/64! Net als Pythagoras benaderde Zarlino de intervallen in de toonladder vanuit een wiskundige invalshoek, hoewel hij later ook de natuurkundige (moderne) basis van de intervallen erkende. 1 Op basis van de getallen 1 t/m 6, het "numero senario", construeerde Zarlino een zuivere "reine" toonladder. Alle getalscombinaties binnen het "numero senario" leverden volgens Zarlino consonanten op. 2 De notatie is in trappen aangegeven (C-Majeur: I=C VII=B).
| I | II | III | IV | V | VI | VII | I |
|---|---|---|---|---|---|---|---|
| 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 |
De reine toonladder van Zarlino is een handleiding voor het zuiver spelen van intervallen. Eenvoudig is dat echter niet! De reine toonladder van Zarlino is een complex bouwwerk met twee typen secundes en twee typen kleine tertsen. De secunde met het interval 9/8 en de kleine terts met het interval 32/27 kennen we van de toonladder van Pythagoras. Het verschil tussen de "Zarlino" en de "Pythagoras" secunde is: 10/9 x 8/9 = 80/81 = -1,23%. Eenzelfde verschil is er tussen de "Zarlino" en de "Pythagoras" kleine tertsen: 6/5 x 27/32 = 81/80 = +1,25%.
| Interval | Rein | Decimaal | +/- Gelijkzw. | |
|---|---|---|---|---|
| Kwint | I-V IV-I | 3/2 | 1,5 | +0,11% |
| Kwart | I-IV III-VI V-I | 4/3 | 1,3333 | -0,11% |
| Grote terts | I-III IV-VI V-VII | 5/4 | 1,25 | -0,79% |
| Kleine terts (Z) | III-V VI-I | 6/5 | 1,2 | +0,91% |
| Kleine terts (P) | II-IV | 32/27 | 1,1852 | -0,34% |
| Secunde (P) | I-II IV-V VI-VII | 9/8 | 1,125 | +0,23% |
| Secunde (Z) | II-III V-VI | 10/9 | 1,1111 | -1,01% |
| Kleine secunde | III-IV VII-I | 16/15 | 1,0667 | +0,68% |
Het fundamentele verschil tussen de toonladder van Pythagoras en die van Zarlino is dat de toonladder van Pythagoras een regelmatig bouwwerk is met 12 gelijke halve toonsafstanden in een octaaf, terwijl de toonladder van Zarlino drie verschillende toonsafstanden heeft (9/8, 10/9, 16/15), die niet passen op een raster van gelijke halve toonsafstanden. Voor toetsinstrumenten is dat een probleem. Stel dat we een piano zuiver zouden stemmen volgens Zarlino, dan is het uitsluitend mogelijk om zuiver te spelen in de toonsoorten C-Majeur en A-Mineur. In D-Majeur zouden we het eerste interval I-II al meteen vals spelen: 10/9 i.p.v. 9/8. En hoe moeten we de zwarte toets F# stemmen voor het zuivere interval II-III? Om zuiver volgens Zarlino te kunnen spelen, zouden we toetsinstrumenten dus voor elke toonsoort moet herstemmen! Met moderne software synthesizer gebaseerde instrumenten zou dit in principe te realiseren zijn, maar in het algemeen is dit voor toetsinstrumenten natuurlijk geen begaanbare weg! Zuiver spelen volgens Zarlino is dus vooral weggelegd voor instrumenten, waar de speler de tonen vrij kan kiezen zonder aan een raster gebonden te zijn, zoals een viool, een trombone of de menselijke stem.
Onzuivere compromissen
In de voorbije eeuwen zijn er diverse stemmingen bedacht teneinde een klavier zo zuiver mogelijk te laten klinken, zoals de "middentoon" stemming, die de twee typen secundes van Zarlino in het midden samenbrengt. 3 Al deze stemmingen zijn compromissen. Het is onmogelijk een stemming te construeren, waarmee in alle toonsoorten alle intervallen volmaakt zuiver klinken! Uiteindelijk is de gelijkzwevende stemming met 12 gelijke halve toonsafstanden van 21/12 de standaard geworden, weliswaar niet voor alle intervallen even zuiver, maar wel voor alle toonsoorten even onzuiver!
Ook zijn er experimenten gedaan met klavieren voorzien van 19 of zelfs 31 toetsen per octaaf. Bekend is het 31-toons Fokker-orgel. Met dit orgel kunnen 1/5 toonsafstanden gespeeld worden. 4 Een praktische oplossing voor orgels en keyboards is de onzuiverheid te camoufleren via vibrato.
Conclusie
Stapelen van kwinten volgens Pythagoras is een doeltreffende methode om diatonische toonladders te construeren, zoals de pentatonische, hexatonische, en heptatonische toonladders. Door twaalf kwinten te stapelen kan de chromatische toonladder (12 halve toonsafstanden) worden geconstrueerd. Een stapeling van kwinten zal echter nimmer tot een veelvoud van octaven leiden, aangezien geen enkele macht van drie deelbaar is door twee (Pythagoreïsche komma). Dit is op te lossen door de kwint met 0,11% te verkleinen van 3/2 naar 27/12 (1,4983). Een sterk punt van de toonladder van Pythagoras is de evenredige verdeling van het octaaf in halve toonsafstanden. Dit maakt het mogelijk om een muziekstuk één of meer halve toonsafstanden te verhogen of verlagen (transponeren), zonder de muziekinstrumenten te herstemmen.
Hoewel met elke volgende kwintenstap het verband met de grondtoon minder duidelijk wordt (complexe breuken), is het niet zo dat na elke volgende kwintenstap de consonantie met de grondtoon afneemt. Doordat de breuken 81/64 en 27/16 na de 4e resp. de 3e kwintenstap dicht bij de verhoudingen 5/4 resp. 6/5 liggen, zijn de tonen E en A consonanter t.o.v. de grondtoon C dan de D na de 2e kwintenstap.
Gioseffo Zarlino (16e eeuw) verfijnde de wiskundige constructie van Pythagoras door de toonladder op basis van de getallen 1 t/m 6 (numero senario) te construeren. De terts kreeg een eigen verhouding (5:4) en daarmee brak Zarlino met de terts van Pythagoras als de som van twee secundes (81/64). Het fundamentele verschil tussen de toonladder van Zarlino en die van Pythagoras is dat de toonladder van Zarlino met drie verschillende toonsafstanden (9/8, 10/9, 16/15) geen regelmatig bouwwerk is met 12 gelijke halve toonsafstanden in een octaaf! Voor toetsinstrumenten is dat een probleem. Bij transponeren zijn de intervallen niet zuiver (vals), oftewel het spelen van intervallen in andere toonsoorten dan C-Majeur en A-Mineur is niet zuiver.
Hoewel er in de voorbije eeuwen diverse stemmingen zijn bedacht om een klavier zo zuiver mogelijk te laten klinken, is uiteindelijk het compromis, de "gelijkzwevende stemming" met 12 gelijke halve toonsafstanden van 21/12, de standaard geworden. In de gelijkzwevende stemming zijn weliswaar niet alle intervallen even zuiver, maar wel in alle toonsoorten even onzuiver! Een praktische oplossing voor orgels en keyboards is de onzuiverheid te camoufleren via vibrato.